AN INTRODUCTION TO THE SCALES OF MT MERU
AND OTHER RECURRENT SEQUENCE SCALES
~Comments and Questions welcome~
This page is an introduction to the series of scales found in this section of the Wilson Archives
http://anaphoria.com/wilsonmeru.html
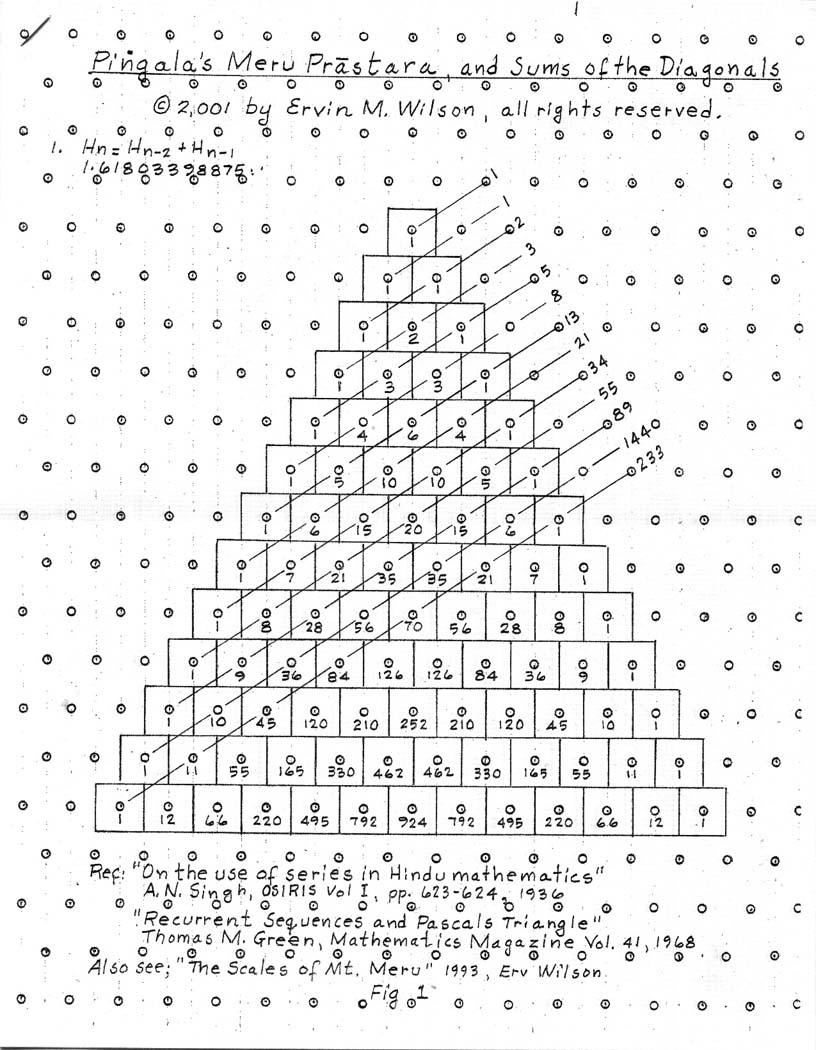
There is no figure more significant to Wilson than Pascal’s Triangle which mysteriously appeared in many of his various tuning developments. Paul Beaver pointed out to him years ago that the Chinese had been pouring over Pascal’s Triangle for thousands of years. Here, Wilson prefers to use its ancient Indian name, Mt Meru, in reference to Meru Prastara. Wilson observed that number sequences found on Mt Meru formed patterns with an uncanny resemblance to scales found in the Far East, Indonesia and even Africa. These are also places where the people hold the legendary mountains of this name in great reverence.
The discovery of this family of scales began via Lou Harrison, who brought to Wilson's attention the Thomas M Green article (Mathematics Magazine Vol. 41 1968) that illustrated how the sum of the simplest diagonal of Mt Meru (Pascal’s Triangle) results in the Fibonacci series and that the sums of other diagonals likewise generated other recurrent sequences, each with its own convergence.
Wilson appears to be the first to investigate these other diagonals and
their recurrent sequences musically. He found this
hard to believe and thought that someone in India or China must have also investigated these diagonals. Regardless of their history, musical appications when treated as a converged ratio, or as a harmonic or subharmonics series produce scales
that are unique in result and approach.

Meru #1 of Mt. Meru (http://www.anaphoria.com/meru.pdf), coresponds with Thomas M Green's diagonal. The series of numbers on the right is the sum of the numbers of the diagonal path but also the sum of the two previous numbers.
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233,etc. being the result of : 1+1 =2, 1+2=3, 2+3=5, 3+5=8 etc. our classic Fibonacci series credited to
Leonardo of Pisa. Why this series is interesting is that the proportion of the two
adjacent terms slowly begins to converge on a particular size,
called the Golden Mean or Golden Proportion, which is
1.61803398875....
This series can be notated in a variety of ways. One is simply as A+B=C or as we see on our sheet toward the upper left Hn=Hn-2+Hn-1 (the standard mathematical formula which is Hn=Hn-x+Hn-y). Wilson drew diagonals at different angles through Mt Meru, and indicated the sums of the numbers in each diagonal to the side of the Meru Triangle. These sums in turn also form recurrent sequences, which we will illustrate.
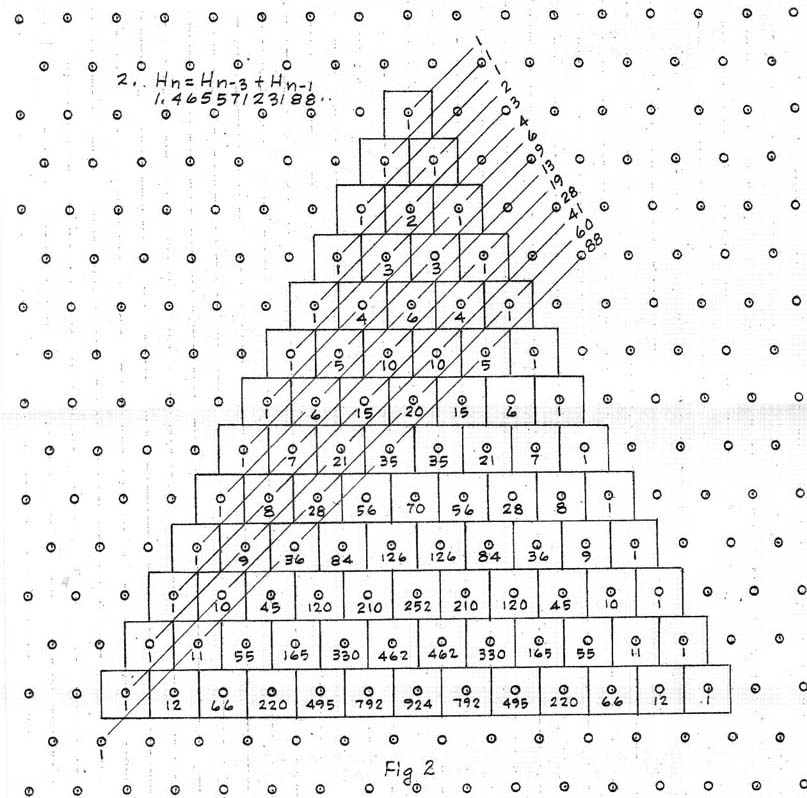
Now, if we look at Meru #2, the recurrent sequence
1, 1, 1, 2, 3, 4, 6, 9, 13, 19, 28, etc.,
requires 3 terms to start (which Erv
calls the seed) and we add the first and third numbers together
(Hn=Hn-3+Hn-1) or (A+C=D). For example, starting with the seed 1, 1, 1, we get 1+1=2, 1+2=3, 1+3=4, 2+4=6, 3+6=9 etc.
This gives us, like before, a series which converges on a
particular proportion, 1.4655712318. Wilson later called this series Meta-Pelog. He used the label 'Meta' to mean 'like'. He would say he did not assume to comprehend how the original family of scales were tuned, but this was his method when he wanted to make a similar scale.
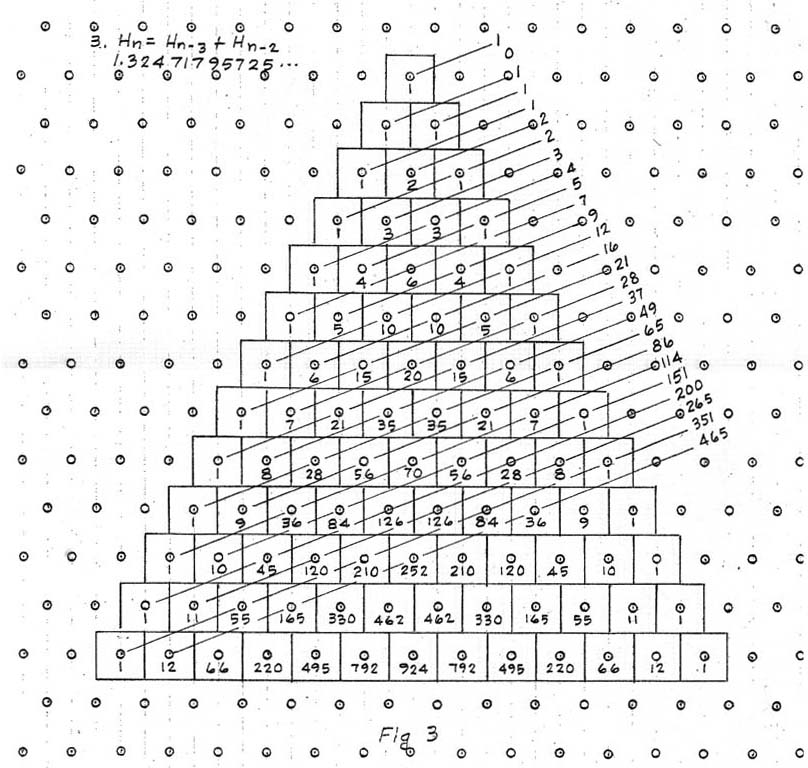
This next diagonal Hn=Hn-2+Hn-3, (or A + B = D) is a scale he
called 'Meta-Slendro' because
it sounds similar to the slendro family of Indonesian scales.

These charts are followed by
illustrations of various zigzag patterns like the one above. It shows the various Moments of
Symmetry (MOS) produced by the convergent ratio. For those not familiar with these and the zigzag patterns, see here. The bottom number of the fraction represents the total
number of scale steps while the top number represents the size of the
generating interval. The fractions also are a guide for mapping the scales on a generalized keyboard. In the above diagram, 3/7 refers to a scale of 7 notes of which the generating
interval will be 3 steps in this scale. The next would be a
12-tone scale in which the generator is 5 steps, etc. Often, Wilson uses a ! (or less commonly an underline) to indicate an MOS that is close to an ET. He also shows the degree of deviation from an ET to the side. These zigzag patterns should be understood as specific locations upon the Scale Tree.
It is worth highlighting the properties that make these scales unique. Harmonically, they have the property of forming a series of proportional (or equal-beating) triads that in turn
generate difference tones
that occur in the scale or its seed. Thus, these scales are constantly
reinforcing themselves, making a self-contained acoustical and
perceivable structure. The proportional triad is found in the sum
triplet by placing the top tone in between the two numbers we used to
generate it. For instance, in Meru #3, we have 16 + 21 = 37. If the two lower numbers are raised an octave (by doubling, i.e. 16 x 2 = 32, 21 x 2 = 42), we get three numbers that form the triad 32:37:42. Each of these numbers are
separated by 5, hence resulting in an equal beating triad. This number 5 is also found in our recurrent sequence.
Next in the sequence, we
have 21 + 28 = 49. If we raise the 21 and 28 up an octave to 42 and 56, we get the triad 42:49:56. The difference tone 7 is the next number in the series following 5. In other words, successive proportional triads will have difference tones that appear consecutively as numbers in the numerical series. Further
properties of the sum triplet to the proportional triad were developed by Wilson in
later papers.
The decision as to where in the numerical series we might start our scale presents us with a musical and artistic choice as opposed to
strictly mathematical determinants. The beginning seed rarely gives us a real cue as to where the scale will end up when it gets closer to converging. Wilson compared it to how when a seed grows into a plant, the seed
disappears or is discarded in the sprout or shoot, and so it is the case when we discard the beginnings of our series to form scales using these
numerical sequences. Depending on how many steps our recurrent sequence spans,
it is only after so many steps will we truly feel the individual
quality of
the sequence as it begins to make itself known. While we could easily wait until the series
converges to the point where the differences between successive numbers
are small, often the most musically interesting parts of these series
lie before this area, when the sequence is in the ballpark, so to
speak, and has not completely narrowed to small fluctuations. A good guide would be to check if the starting point fits well into the same keyboard pattern as the convergd generator. Even
within a single series seeded by the same numbers, different people can
choose different starting places. I would recommend starting
low and proceeding upward. More often than not, I end up settling a bit
higher than where I start the first time. Others might have quite
different and maybe even opposing experiences so it really is wide open.
Jacques Dudon independently and concurrently worked and developed many of these series. He used a method of finding what he calls the P series. This can be found by multiplying the converged generator by the set of ascending whole numbers at least up to the number of seed numbers needed and rounding out the results.
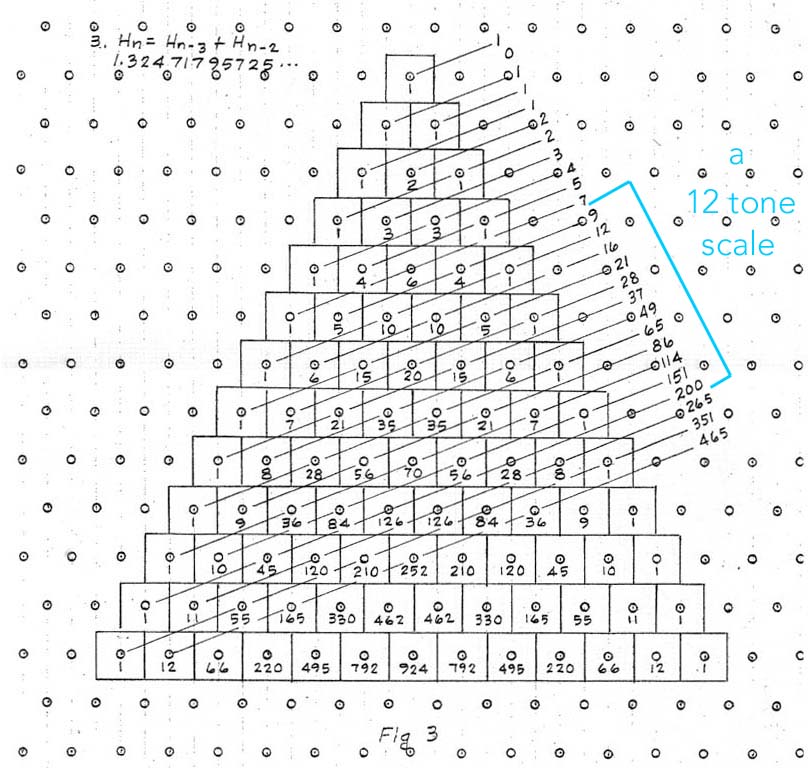
Let us take Meru #3 Meta-Slendro as an example of
applying the above. It is the Meru scale that I have used most, having built an orchestra of instruments as well as composing numerous
pieces and shadow plays. I begin my tuning on 9 and
proceed up to 200, which produces 12 different pitches. The
variety available enables each basic pentatonic to produce
different intervallic variations. Most recently my Escalade instrument fills out the gaps in the scale, producing a 37-tone extension. The instrument is made out of various glockenspiel bars that are laid out to produce glissandos, if desired. Some instruments now take the scale to 17 tones with 816 being the highest harmonic.
The other possibility would be to take the interval upon which
the infinite series converges, as shown by Erv on each zigzag page. In
the case of Meta-Slendro, this is 1.32471795725... which one would want to convert to its log base
2 value (often also included on the zigzag page). The advantage of using the converged ratio is that the
subharmonic and harmonic versions are the same and the basic triad
produced by the scale will be usable in both forms. The disadvantage
is a lack in variation in scale shape. Traditionally, people seem to
prefer unequal size steps in their scales to equal ones.
The numerical seed also offers a myriad of variations as one can
seed these recurrent series how one wishes. Another Meru #3 seed that Wilson was
quite fond of starts with 10, 13, 17, 23, 30, 40, 53, 70, 93, etc.
One can also seed the Mt Meru triangle with different numbers which can be found here.The
real importance of this method is that it allows for each individual
to make their own Slendro, in much the same way a different village
might do so in Indonesia. This makes it difficult to put down in stone,
or in Scala, the most definitive version of the scale. It should
be understood that each of these are only representatives of a whole family of
scale possibilities. Each slant likewise should be understood as a genus of scales,
open to such seeding.
Also, there are various recurrent sequences beyond the Mt Meru triangle. These are generated from seed values in different octave multiples from those found on the triangle. They include scales
such as Meta-Meantone and Meta-Mavila.
There is an extended mapping of EXTENDED DIAGONALS AND VARIOUS PRIMARY AND SECONDARY RECURRENT SERIES which extends the series
here http://anaphoria.com/secondaryrecurrents.html
~Comments and Questions welcome~