Copan

(Found in Copan is a Double-headed Stone Dragon of the Mayans. Like the two heads, this scale encompasses two series, and by coincidence it is in the year of the dragon and the end of the Mayan Calender that is finding its first use.) It was first presented and dedicated to Billy Stiltner.

Musically the scale tends to cluster around notes in the vicinity ef 8 'equal' so can have a type of dual diminished quality making the scale easily useful for the dark and forboding without resolution. The scale converges on a generator of 751.659~ cents that could be used to construct a 'golden version' of the scale by superimposing it is the most accurate at ones disposal. Copan forms good Moments of Symmetries at (1, 3, 5) 8, 11, 19, 27, 35, 43, 51, 59, 67, 75, 83 etc. What is explained below is a version based on seeding it with harmonics as I prefer the numerical sequence versions of Meru-like scales.

This composition in progress , A Molten Wind is a 19 minute example. It now nevertheless is under major revisions and should be taken only as an example of the scales character.

Originally there were found two recurrent sequences that generated this scale with two proportional triads as chords or sonorities.

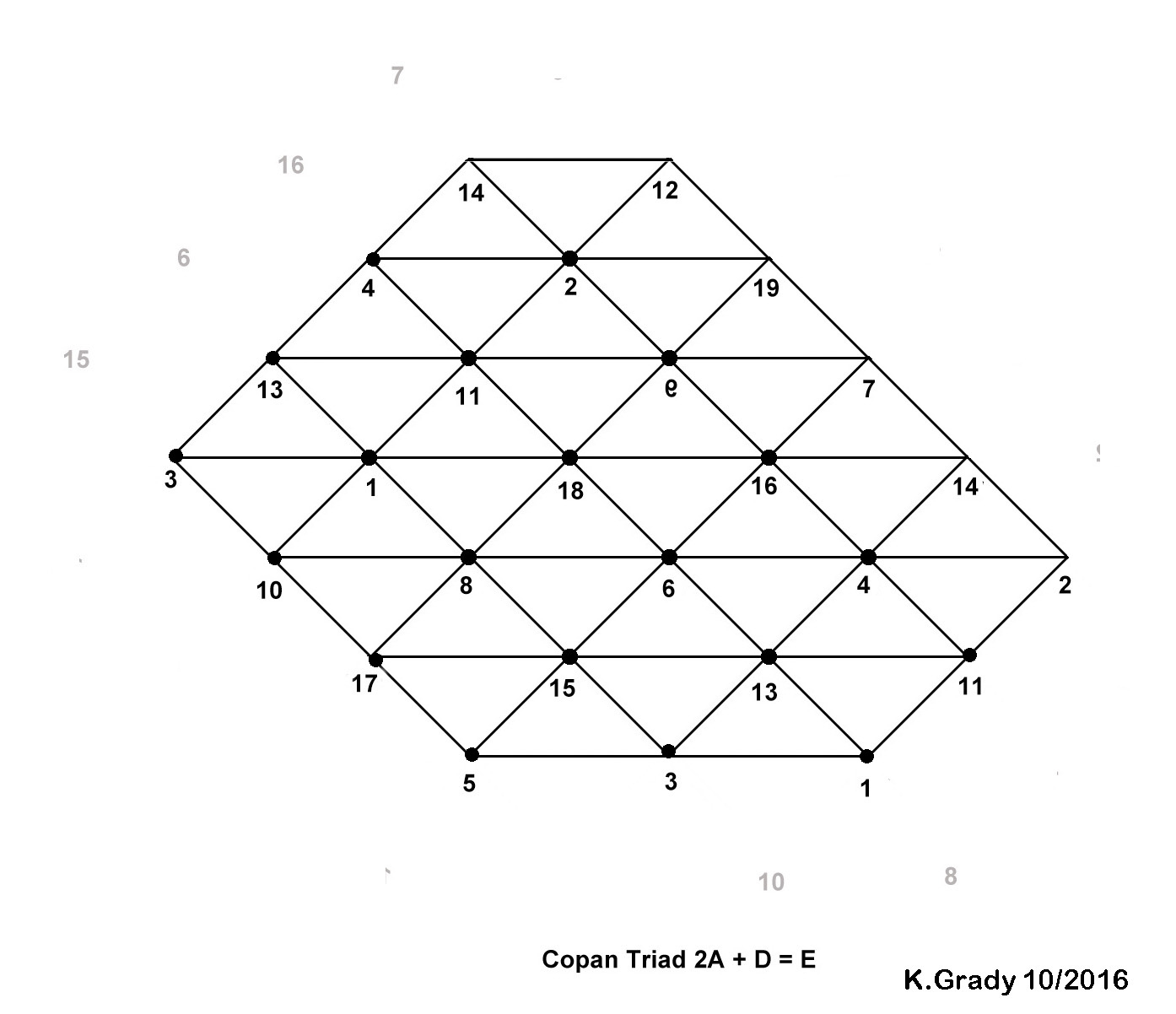
Hn = 2Hn-4 + Hn-1 [one can also express as ( 2A + D = E )

and

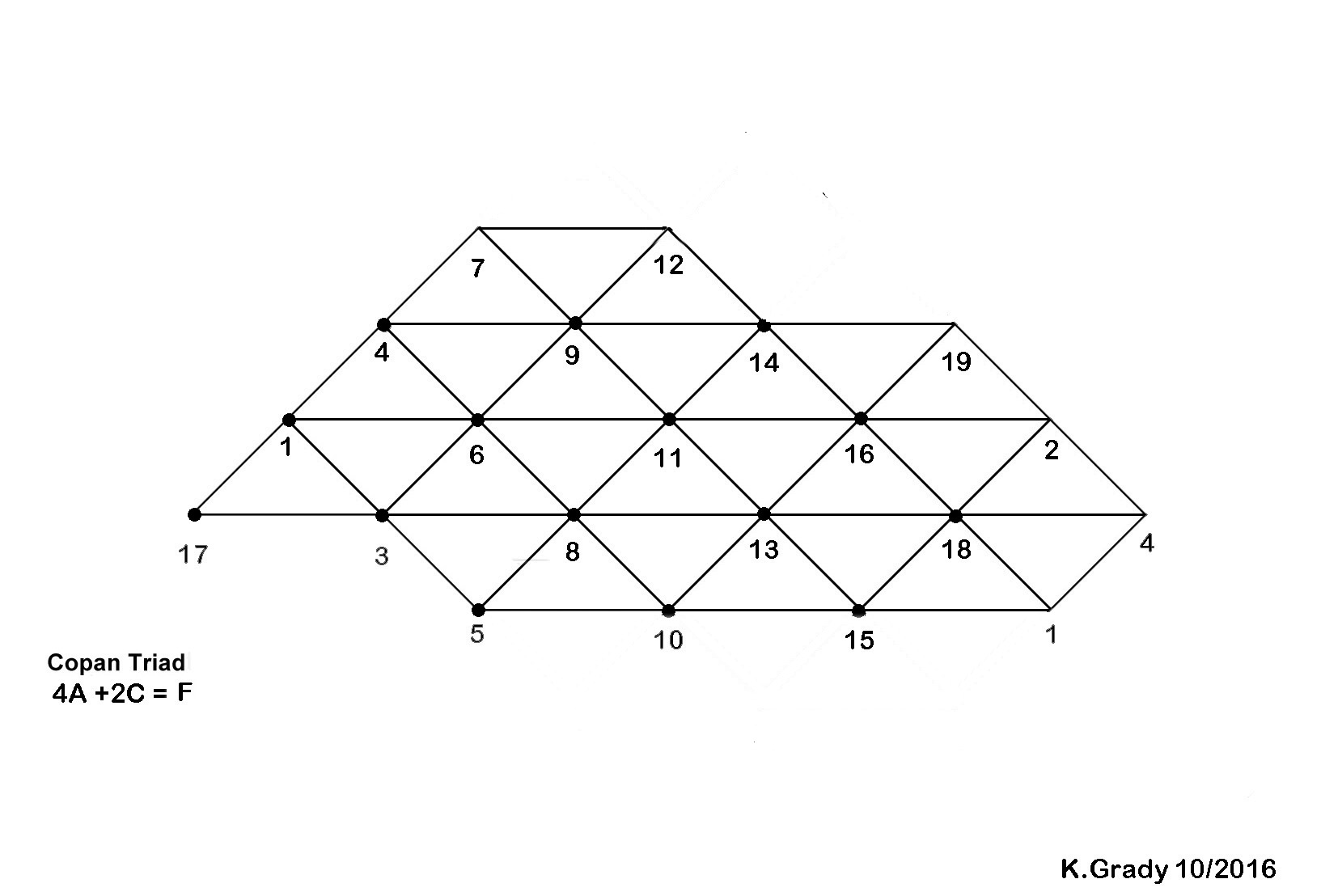
Hn = 4Hn-5 + 2Hn-3 ( 4A + 2C = F )

But two other recurrent sequences have now also been found bringing the number to 4.

the other two are

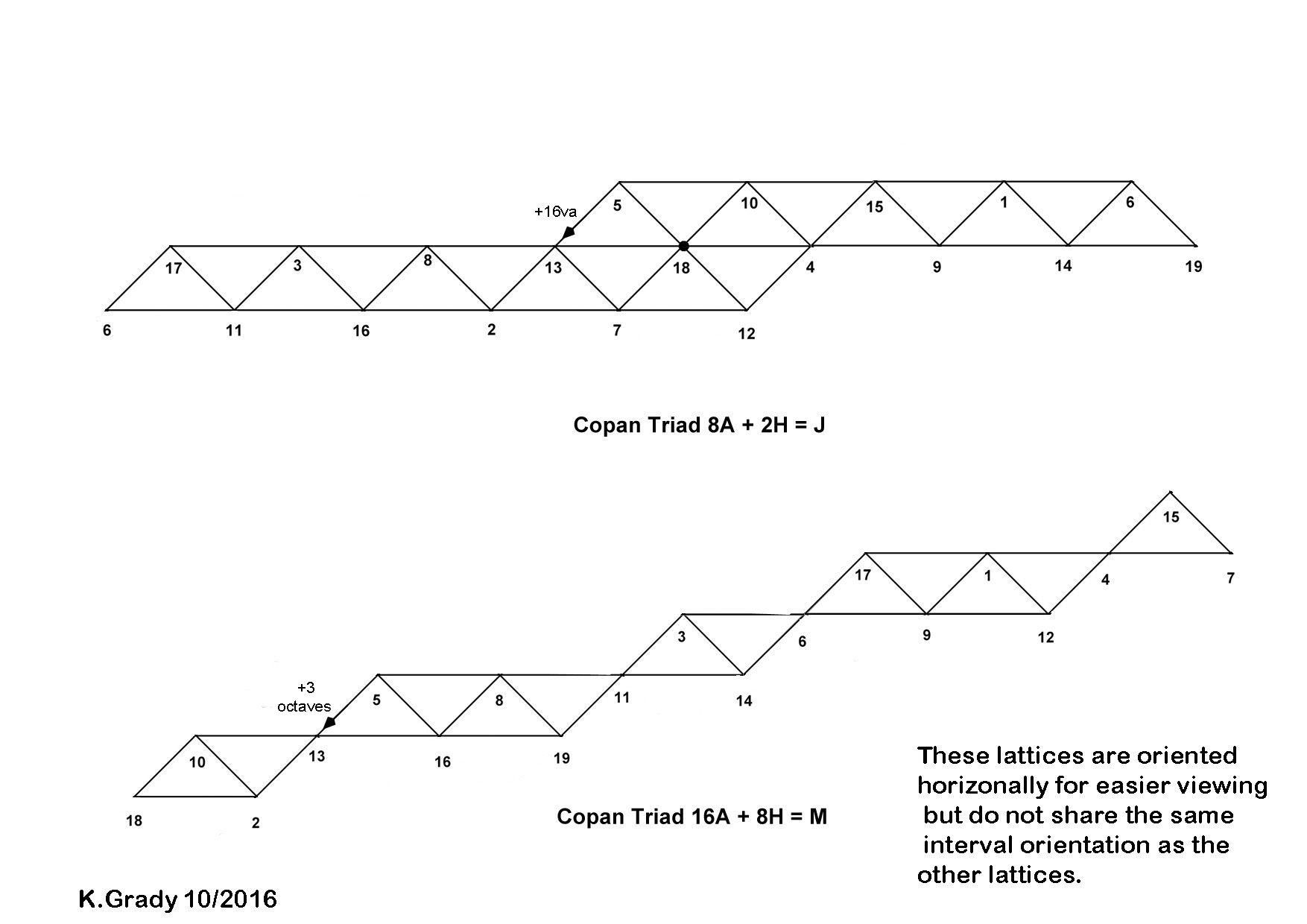
Hn = 8Hn-9 + 2Hn-2 ( 8A + 2H = J )

............example 116 x 8= 928

..........................................+

.....................2420 x 2 = 4840

................928 + 4840 = 5768

and

Hn = 16Hn-12 + 8Hn-5 ( 16A + 8H = M )

............example 116 x 16= 1856

..............................................+

............example 2420 x 8 = 19360

........................................= 21216

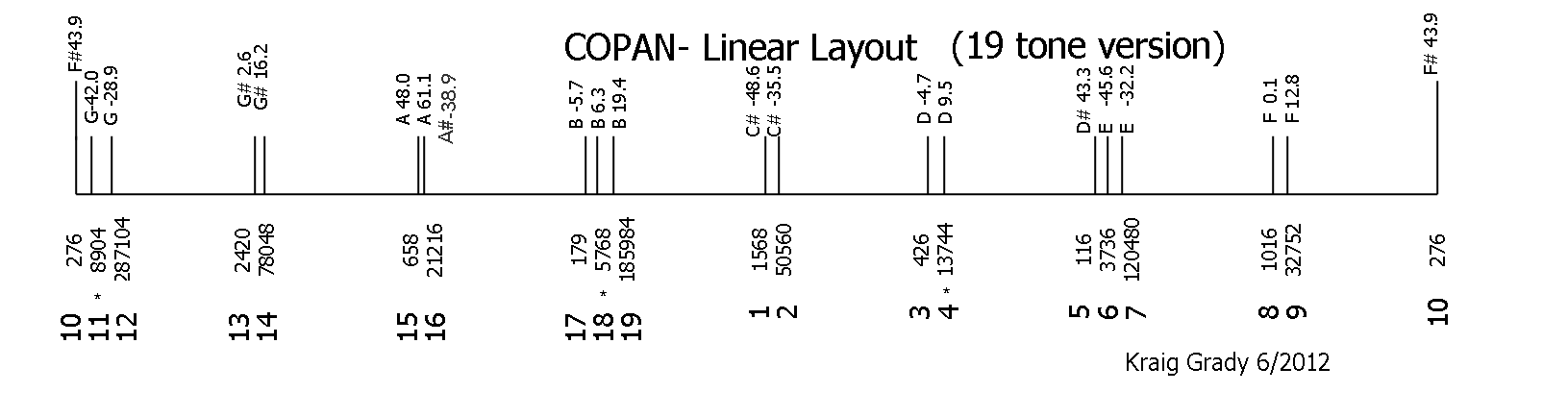
In this instance, I seeded the scale with harmonics as follows. I include the resultant scale step numbers (x.) in a 19 tone scale in order to facilitate details the reader might wish to pursue.

(5.) 116 seed beginning

(17.) 179

(10.) 276

(3.) 426 seed to first formula carried to here ( in example 116 times 2 + 426 = 658)

(15.) 658 seed to second formula carried to here ( in example 276 times 4 + 658 times 2 = 2420)

8.) 1016

(1.) 1568

(13.) 2420 seed to both third and forth formulas ( in different octaves )

(6.) 3736

(18.) 5768

(11.) 8904

(4.) 13744

(16.) 21216

(9.) 32752

(2.) 50560

(14.) 78048

(7.) 120480

(19.) 185984

(12.) 287104

copanchart

While each Moment of Symmetry occurs in multiple rotations, the simplest can be found with the 8 tone one unmarked on the left of each group, with the 11 requiring the addition of an *.

The 8 tone is marked *, with the 11 requiring the addition of +

The complement to * is also an 11 and the complement to * and + 11 is another 8 tone

*=8 tone, add+ = 11 tone

Building proportional triads on the lowest tone of our series results in these examples in terms of scale step numbers

5. 3. 15.
5. 10. 8.
5. (+2 octaves ) 13. 18.
5. (+3 octaves ) 13. 16.

In this 19 tone scale, only the following transpositions are possible.

2A + D = E
5.	3	15.
17.	15.	8.
10.	8.	1.
3.	1.	13.
15.	13.	6.
8.	6.	18.
1.	18.	11.
13.	11.	4.
6.	4.	16.
18.	16.	9.
11.	9.	2.
4.	2.	15.
16.	14.	7.
9.	7.	19.
2.	19.	12.

4A + 2C = F
5.	10.	8.
17.	3.	1.
10.	15.	13.
3.	8.	6.
15.	1.	18.
8.	13.	11.
1.	6.	4.
13.	18.	16.
6.	11.	9.
18.	4.	2.
11.	16.	14.
4.	9.	7.
16.	2.	19.
9.	14.	12.

8A + 2H = J
5.(+2 octaves )	13.	18.
17.	6.	11.
10.	18.	4.
3.	11.	16.
15.	4.	9.
8.	16.	2.
1.	9.	14.
13.	2.	7.
6.	14.	19.
18.	7.	2.

16A + 8H = M
5.(+3 octaves )	13.	16.
17.	6.	9.
10.	18.	2.
3.	11.	14.
15.	4.	7.
8.	16.	19
1.	9.	12.

IN THE TABLES BELOW

3, 5 , 6 = 2A + D = E

2, 3, 5 = 4A + 2C = F

1, 2, 3 = 8A + 2H = J

1, 4, 5 = 16A + 8H = M

5.(+2 octaves )	13.	18.	13.	16.	9.
17.	6.	11.	6.	9.	2.
10.	18.	4.	18.	2.	14.
3.	11.	16.	11.	14.	7.
15.	4.	9.	4.	7.	19
8.	16.	2.	16.	19	12.

...............................3.............5.......6

......................2.......3.............5

1.....................2.......3

1.....................................4......5

THIS CHART SHOWS THE EXTENT OF THE

PRESENTS OF TRIADS WITH USING THE SPACING

FOUND ABOVE

		5.		3.	15.	+
		17.		15.	8.	+
	5.	10.	5.	8.	1.	+0
	17.	3.	17.	1.	13.	+1
	10.	15.	10.	13.	6.	+2
	3.	8.	3.	6.	18.	+3
	15.	1.	15.	18.	11.	+4
	8.	13.	8.	11.	4.	+5
	1.	9.	1.	4.	16.	+6
5.	13.	18.	13.	16.	9.	+7
17.	6.	11.	6.	9.	2.	+8
10.	18.	4.	18.	2.	14.	+9
3.	11.	16.	11.	14.	7.	+10
15.	4.	9.	4.	7.	19	+11
8.	16.	2.	16.	19	12.	+12
1.	9.	14.	9.	12.		+13
13.	2.	7.	2.
6.	14.	19	14.
18.	7.	12.	7.

.....................3................5.......6

............2.......3................5

1..........2.......3

1............................4.......5

These charts show proportional triadunder each recurrent by step size.

Copan triads of 2A+D=E

Copan triads of 4A+2C=F

Copan triads of 2 other recurrents

Once I have looked at and listened to all of these, I pretty much compose by ear but don't regret being informed by looking at these simpest structures (they are just triads regardless of what the numbers say) within the tuning. Thanks if you made it this far.

coffeeman

5.	3	15.
17.	15.	8.
10.	8.	1.
3.	1.	13.
15.	13.	6.
8.	6.	18.
1.	18.	11.
13.	11.	4.
6.	4.	16.
18.	16.	9.
11.	9.	2.
4.	2.	15.
16.	14.	7.
9.	7.	19.
2.	19.	12.

5.	10.	8.
17.	3.	1.
10.	15.	13.
3.	8.	6.
15.	1.	18.
8.	13.	11.
1.	6.	4.
13.	18.	16.
6.	11.	9.
18.	4.	2.
11.	16.	14.
4.	9.	7.
16.	2.	19.
9.	14.	12.

		5.		3.	15.	+
		17.		15.	8.	+
	5.	10.	5.	8.	1.	+0
	17.	3.	17.	1.	13.	+1
	10.	15.	10.	13.	6.	+2
	3.	8.	3.	6.	18.	+3
	15.	1.	15.	18.	11.	+4
	8.	13.	8.	11.	4.	+5
	1.	9.	1.	4.	16.	+6
5.	13.	18.	13.	16.	9.	+7
17.	6.	11.	6.	9.	2.	+8
10.	18.	4.	18.	2.	14.	+9
3.	11.	16.	11.	14.	7.	+10
15.	4.	9.	4.	7.	19	+11
8.	16.	2.	16.	19	12.	+12
1.	9.	14.	9.	12.		+13
13.	2.	7.	2.
6.	14.	19	14.
18.	7.	12.	7.

5.	3	15.
17.	15.	8.
10.	8.	1.
3.	1.	13.
15.	13.	6.
8.	6.	18.
1.	18.	11.
13.	11.	4.
6.	4.	16.
18.	16.	9.
11.	9.	2.
4.	2.	15.
16.	14.	7.
9.	7.	19.
2.	19.	12.

5.	10.	8.
17.	3.	1.
10.	15.	13.
3.	8.	6.
15.	1.	18.
8.	13.	11.
1.	6.	4.
13.	18.	16.
6.	11.	9.
18.	4.	2.
11.	16.	14.
4.	9.	7.
16.	2.	19.
9.	14.	12.

		5.		3.	15.	+
		17.		15.	8.	+
	5.	10.	5.	8.	1.	+0
	17.	3.	17.	1.	13.	+1
	10.	15.	10.	13.	6.	+2
	3.	8.	3.	6.	18.	+3
	15.	1.	15.	18.	11.	+4
	8.	13.	8.	11.	4.	+5
	1.	9.	1.	4.	16.	+6
5.	13.	18.	13.	16.	9.	+7
17.	6.	11.	6.	9.	2.	+8
10.	18.	4.	18.	2.	14.	+9
3.	11.	16.	11.	14.	7.	+10
15.	4.	9.	4.	7.	19	+11
8.	16.	2.	16.	19	12.	+12
1.	9.	14.	9.	12.		+13
13.	2.	7.	2.
6.	14.	19	14.
18.	7.	12.	7.

5.	3	15.
17.	15.	8.
10.	8.	1.
3.	1.	13.
15.	13.	6.
8.	6.	18.
1.	18.	11.
13.	11.	4.
6.	4.	16.
18.	16.	9.
11.	9.	2.
4.	2.	15.
16.	14.	7.
9.	7.	19.
2.	19.	12.

5.	10.	8.
17.	3.	1.
10.	15.	13.
3.	8.	6.
15.	1.	18.
8.	13.	11.
1.	6.	4.
13.	18.	16.
6.	11.	9.
18.	4.	2.
11.	16.	14.
4.	9.	7.
16.	2.	19.
9.	14.	12.

		5.		3.	15.	+
		17.		15.	8.	+
	5.	10.	5.	8.	1.	+0
	17.	3.	17.	1.	13.	+1
	10.	15.	10.	13.	6.	+2
	3.	8.	3.	6.	18.	+3
	15.	1.	15.	18.	11.	+4
	8.	13.	8.	11.	4.	+5
	1.	9.	1.	4.	16.	+6
5.	13.	18.	13.	16.	9.	+7
17.	6.	11.	6.	9.	2.	+8
10.	18.	4.	18.	2.	14.	+9
3.	11.	16.	11.	14.	7.	+10
15.	4.	9.	4.	7.	19	+11
8.	16.	2.	16.	19	12.	+12
1.	9.	14.	9.	12.		+13
13.	2.	7.	2.
6.	14.	19	14.
18.	7.	12.	7.